Обичне и децималне фракције и поступци над њима

Већ у основним школама се суочавајуфракције. И онда се појављују у свакој теми. Не можете заборавити акције са овим бројевима. Стога морате знати све информације о обичним и децималним фракцијама. Ови концепти су једноставни, главна ствар је разумјети све у реду.

Зашто вам требају фракције?

Свијет око нас састоји се од цијелих предмета. Стога у акцијама нужности нема. Али свакодневни живот непрестано гурује људе да раде са деловима ствари и стварима.

На пример, чоколада се састоји од неколико лобула. Размотрите ситуацију када је плочица формирана дванаест правоугаоника. Ако је подељен на два, онда се испоставља да је 6 делова. Она ће бити добро подељена на три. Али пет неће моћи да дају читав низ чоколадних резина.

Иначе, ови сегменти су већ фракције. А њихова даља подела доводи до појаве сложенијих бројева.

Шта је "фракција"?

Овај број се састоји од делова јединице. Вањски изгледа као два броја одвојена хоризонталном или косом. Ова карактеристика се назива фракционим. Број написан горе (лево) назива се бројац. Оно што стоји одоздо (са десне стране) је именитељ.

У ствари, фракциона линија је знак поделе. То јест, нумератор се може назвати дељивим, а именитељ се може назвати делитељом.

Које су фракције?

У математици постоје само два типа: обичне и децималне фракције. Са првим ученицима се упознају у основним разредима, називајући их само "фракцијама". Други учимо у 5. разреду. Тада се појављују ова имена.

Обичне фракције су све оне које су написанеоблик два броја раздвојена линијом. На пример, 4/7. Децимални је број у којем фракциони део има позицијску евиденцију и одвојен је од целине зарезом. На пример, 4.7. Студенти морају јасно схватити да су два наведена примера потпуно различита броја.

Свака једноставна фракција се може написати као децимална. Ова изјава је скоро увек тачна у супротном смеру. Постоје правила која вам омогућавају да упишете децималну фракцију са обичним фракцијама.

Које подврсте имају ове врсте фракција?

Почните боље у хронолошком редоследу, јер се оне проучавају. Први су обичне фракције. Међу њима постоји 5 подврста.

1. Тачно. Његов бројац је увек мање од именитеља.

2. Погрешно. Бројач је већи или једнак именику.

3. Редуцибле / унредуцибле. То може бити тачно или нетачно. Још једна важна ствар је да ли бројац са именитељем има заједничке факторе. Ако постоје, тада би требали поделити оба дела фракције, односно, смањити.

4. Мијешано. На његов уобичајени тачан (нетачни) фракциони део, додељен је цијели број. И увек се налази на левој страни.

5. Једињење. Формирана је из две подељене фракције. То јест, она има три фракцијске карактеристике одједном.

Децималне фракције имају само две подврсте:

• финале, односно оне чији је део који је ограничен (има крај);

• бесконачан - број чије се цифре после зареза не завршавају (могу се писати бескрајно).

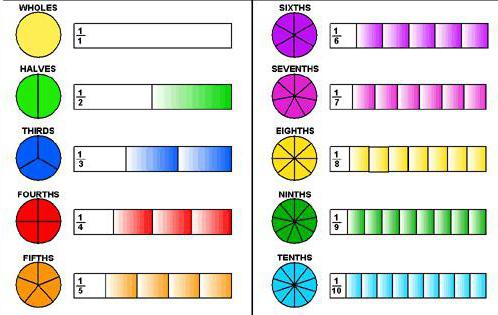
Како конвертовати децимално у обичну фракцију?

Ако је ово коначан број, онда се примењује асоцијација заснована на правилу - као што чујем, па пишем. То јест, морате га исправно прочитати и записати, али без зареза, али са фракционом линијом.

Као кључ о неопходном именитељу, морате запамтити да је увек једна и више нула. Последње потребе треба да пишу цифре у фракционом делу броја који се разматрају.

Како претворити децимале у обичне фракције,ако је њихов цео део одсутан, односно једнак је нули? На пример, 0,9 или 0,05. Након примене овог правила, испоставља се да морате написати нулте интегерс. Али то није прецизирано. Остаје да се записују само фракциони дијелови. За прву, именитељ ће бити 10, а други ће бити 100. То значи да ће наведени примери имати бројеве 9/10, 5/100. А последњи се испоставља да је пресечен са 5. Због тога, резултат треба да буде написан 1/20.

Како направити децималну фракцију,ако је његов цео број различит од нуле? На пример, 5.23 или 13.00108. У оба примера читав део се чита и његова вриједност је написана. У првом случају, ово је 5, у другом случају, 13. Затим морамо ићи на фракциони део. Они требају извршити исту операцију с њима. Први број се појављује 23/100, други - 108/100000. Друга вредност треба поново да се смањи. У одговору се добијају ове мешовите фракције: 5 23/100 и 13 27/25000.

Како конвертовати бесконачно децимално у обичну децималну фракцију?

Ако није периодична, таква операција неће бити могућа. Ова чињеница се односи на чињеницу да је свака децимална фракција увек преведена у крајњу или на периодичну.

Једино што је дозвољено с тимфракције, да је окружи. Али онда ће децимална разлика приближно бити једнака оној бесконачној. Већ се може претворити у обичну. Али обрнути процес: превођење на децимални број никада неће дати почетну вриједност. То значи да бесконачне непериодичне фракције у обичне фракције нису преведене. Морате то запамтити.

Како написати неограничену периодичну фракцију у облику обичног?

У овим бројевима, након зареза,једну или више цифара које се понављају. Зове се период. На пример, 0,3 (3). Овде "3" у том периоду. Они се класификују као рационални, јер се могу претворити у обичне фракције.

Они који су се срели са периодичним фракцијама,познато је да могу бити чисти или мешани. У првом случају, период почиње одмах из зарезе. У другом - фракциони део почиње са било којим бројем, а затим почиње понављање.

Правило којим желите да пишете у формиобична фракција бесконачног децималног броја ће бити различита за две врсте назначених бројева. Чисте периодичне фракције за писање обичних су прилично једноставне. Као и са коначним, они морају бити трансформисани: у нумератору напишите период, а именитељ ће бити број 9, поновљен онолико пута колико број садржи период.

На пример, 0, (5). Цијели део броја није, тако да одмах морате почети фракционо. У нумератору напишите 5, а у именику једног 9. То јест, одговор је фракција од 5/9.

Правило о томе како се записује обична децимална периодична фракција, која је помешана.

• Бројање цифара фракционог дела прије тог периода. Они ће назначити број нула у именитељу.

• Погледајте дужину периода. Толико ће имати именитељ.

• Запишите именитељ: првих девет, затим нула.

• Да бисте утврдили нумератор, морате да упишете разлику два броја. Умањења ће бити све цифре након децималне тачке, заједно са временом. Израчунавање - исто је без периода.

На пример, 0,5 (8) - записати периодичнудецимална фракција у облику обичног. У фракционом делу, до периода постоји једна фигура. Значи нула ће бити једна. У истом периоду, само једна цифра је 8. То је један од девет. То јест, у именитељу је потребно написати 90.

Да бисте одредили нумератор са 58, потребно је да одузмете 5. Испоставља се 53. Одговор на примјер би био да напишете 53/90.

Како су обичне фракције претворене у децимале?

Најједноставнија верзија је број чији је именитељ 10, 100 и тако даље. Онда се именитељ једноставно одбацује, а запета се поставља између фракционих и целих делова.

Постоје ситуације када је именитељ лакСе претвара у 10, 100 и тако даље. Д. На пример, бројеви 5, 20, 25. Они су довољно помножен 2, 5 и 4, респективно. Само умножавају се ослања не само именитељ, већ и бројник од истог броја.

У свим осталим случајевима корисно је једноставно правило: подијелите нумератор за именитеље. У овом случају, можете добити две варијанте одговора: коначни или периодични децимални.

Акције са обичним фракцијама

Додавање и одузимање

Са њима се студенти упознају са другима. Прво, фракције имају исте ознаке, а онда другачије. Општа правила могу се смањити на такав план.

1. Нађите најмање заједничко вишеструко именовање.

2. Напишите додатне факторе за све обичне фракције.

3. Помножите нумераторе и деноминаторе према факторима који су њима одређени.

4. Додајте (одузмите) нумераторе фракција и оставите заједнички именитељ непромењен.

5. Ако је бројац смањеног мањи од субтрахенде, онда морамо сазнати да ли имамо мијешани број или одговарајућу фракцију.

6. У првом случају, цео део треба да заузме јединицу. Додајте именитељ у бројац фракције. И онда изврши одузимање.

7. У другом - неопходно је примијенити правило одузимања од мањег броја. То јест, одузмите модул из модула за подмазивање и одговорите на знак "-".

8. Пажљиво погледајте резултат додавања (одузимање). Ако се добије неправилна фракција, онда је неопходно додијелити цијели дио. То јест, да се бројевач подели именитељем.

Множење и поделу

Да би их извршили, фракције не морају довести до заједничког именитеља. Ово поједностављује извршење акција. Али они и даље морају поштовати правила.

1. Када се множе обичне фракције, потребно је узети у обзир бројеве у нумераторима и именитељима. Ако било који нумератор и именитељ имају заједнички мултипликатор, они се могу смањити.

2. Помножите нумераторе.

3. Помножите именитеље.

4. Ако се испостави да је редукована фракција, онда би требало поново бити поједностављена.

5. Када се дели, прво морамо да заменимо поделу множењем, а делилац (друга фракција) обрнутим делом (заменимо нумератор и именитељ).

6. Онда поступите као размножавање (почевши од тачке 1).

7. У задацима у којима морате размножити (поделити) цео број, ово би требало да буде написано у облику погрешног дела. То јест, са именитељем 1. Онда поступите као што је горе описано.

Акције са децималима

Додавање и одузимање

Наравно, увек можете да окренете децимално местоу обичној. И поступите према већ описаном плану. Али понекад је погодније деловати без овог превода. Онда ће правила за њихову додељивање и одузимање бити потпуно иста.

1. Изједначите број цифара у фракционом делу броја, то јест, након децималне тачке. Додијелите недостајући број нула у њему.

2. Напишите фракцију тако да је запета под зарезом.

3. Додајте (одузмите) као природне бројеве.

4. Скините зарез.

Множење и поделу

Важно је да не морате додавати нуле овдје. Фракције треба да буду остављене како су дате у овом примеру. А онда идите према плану.

1. Да бисте се множили, морате да пишете фракције један испод друге, не обраћајући пажњу на записе.

2. Множите, као природни бројеви.

3. Ставите зарез у одговор, рачунајући са десног краја одговора онолико бројева колико су они у делимичним деловима оба мултипликатора.

4. Да бисте поделили, прво морате претворити делитељ: учинити га природним бројем. То јест, помножите га са 10, 100, итд, у зависности од тога колико је цифара у фракционом делу делитеља.

5. Да увећате дивиденду за исти број.

6. Поделите децимални број у природни број.

7. Ставите зарез у одговору у тренутку када је цео део завршен.

Шта ако у једном примеру постоје обе врсте фракција?

Да, у математици, често постоје примери, укоје треба да извршавају радње на обичним и децималним фракцијама. У таквим задацима постоје два могућа решења. Неопходно је објективно мерити бројеве и изабрати оптималну.

Први пут: увести обичну децималну

Погодно је, ако делите или преведетеКоначне фракције се добијају. Ако бар један број даје периодни део, онда је овај метод забрањен. Стога, чак и ако не волите да радите са обичним фракцијама, мораћете да их бројате.

Други начин: да запишете децимале обичним

Ова метода је погодна ако је делимичнонакон децималног броја има 1-2 цифре. Ако их има више, можете добити веома велику обичну фракцију и децималне ознаке ће вам омогућити да брже и лакше пребројите задатак. Због тога, увек морате трезно процијенити задатак и одабрати најједноставнији метод рјешења.