Боолеан алгебра. Алгебра логике. Елементи математичке логике

У савременом свету, ми све више користиморазних машина и уређаја. И не само када је неопходно применити буквално натприродну снагу: померите рад да га подигне на висину, копају дуге и дубоке ровове, итд Аутомобили данас прикупљају роботи, храна се кува Мултиварки и основних израчунавања аритметичке производе калкулаторе ... Све више и чешће чујемо израз "Булова алгебра". Можда је дошло време да схвати улогу људских бића у стварању робота и машина способност да решава не само математички, већ и логичких проблема.

Логика

На грчком је логиканаредио систем мисли да ствара однос између датим условима и омогућава вам да закључке на основу претпоставки и процјена. Често се питамо једно друго: "Да ли је логично?" Одговор одговара нашим претпоставкама или критикује ток мисли. Али тај процес не заустави ту: настављамо да разговарамо.

Понекад је број услова (уводни) такавсјајно, а међусобне везе између њих су толико збуњујуће и сложене да људски мозак није у стању да "савлада" све одједном. Може потрајати више од мјесец дана (седмица, годину) како би разумијео шта се дешава. Али савремени живот нам не даје такве интервале за доношење одлука. И користимо рачунаре. И ту се појављује алгебра логике, са својим законима и својствима. Након што смо преузели све почетне податке, омогућавамо рачунару да препозна све односе, елиминише контрадикције и пронађе задовољавајуће рјешење.

Математика и логика

Најпознатији Готтфриед Вилхелм Леибнизформулисао концепт "математичке логике", чији су задаци били доступни само уском кругу научника. Посебан интерес у овом правцу није изазвао, а до средине КСИКС века мало је знало о математичкој логици.

Велико интересовање за наукуспор у којем је Енглез Џорџ Бухл објавио своју намеру да створи део математике који није имао никакву практичну примену. Као што се сећамо из историје, у то доба се активно развијала индустријска производња, развијене су све врсте помоћних машина и машина, односно сва научна открића имала су практичну оријентацију.

Гледајући напред, кажемо да је Боолеан алгебра најчешће коришћени део математике у савременом свету. Дакле, спор је изгубио Боуле.

Георге Боуле

Сама личност аутора заслужује посебнупажњу. Чак и узимајући у обзир чињеницу да су у прошлости људи постали старији него што и даље не можемо помислити да је у 16. години Ј. Булл учио у сеоској школи, а до 20 година отворио своју школу у Линколну. Математичар је савршено савладао пет страних језика, ау његовом слободном времену прочитао су дела Њутна и Лагрангеа. А све ово је о сину једноставног радника!

Године 1839. Боуле је прво послао научникарад у Кембриџу Матхематицал Јоурнал. Научник је 24 година. Бул рад је толико заинтересовани чланови Краљевског друштва, 1844. године добио је медаљу за допринос развоју математичке анализе. Неколико објављених радова у којима су елементи математичке логике, математике дозвољено да млади преузме дужност професора на Цоллеге оф Цорк Цоунти су описани. Подсетимо се да у веома Бул образовање није било.

Идеја

У принципу, Боолова алгебра је врло једноставна. Постоје изјаве (логички изрази), који се, с аспекта математике, могу дефинисати само две речи: "истина" или "лаж". На пример, на пролеће дрвеће цвјета - истина, љети снијег - лажи. Сав шарм ове математике јесте да нема строге потребе за кориштењем само бројева. Сви пропозиције са недвосмисленим значењем су савршено погодне за алгебру пропозиција.

Према томе, алгебра логике може битисе користи буквално свуда: у распореду и писању инструкција, анализирајући конфликтне информације о догађајима и одређивању редоследа акција. Најважније је разумети да није важно како смо одредили истину или лажност изјаве. Од ових "како" и "зашто" треба бити апстраховано. Једина ствар која је важна је изјава о чињеници: истина-лажна.

Наравно, функције су важне за програмирањеалгебре логике, које су написане са одговарајућим знаковима и симболима. А да их научи значи савладати нови страни језик. Ништа није могуће.

Основни појмови и дефиниције

Без уласка у дубине, разумемо терминологију. Дакле, Боолова алгебра претпоставља присуство:

• изјаве;
• логичке операције;
• функције и закони.

Изјаве - било који афирмативни израз,које се не могу тумачити двоструко. Они су написани у облику бројева (5> 3) или формулисани уз уобичајене речи (слон је највећи сисар). У овом случају, израз "жирафа нема врат" такође има право да постоји, само Боолова алгебра ће га дефинирати као "лаж".

Све изјаве морају бити јаснекарактер, али они могу бити елементарни и сложени. Други користе логичке везе. То јест, у пропозиционим алгебарским изјавама о саставу се формирају додавањем елементарних елемената кроз логичке операције.

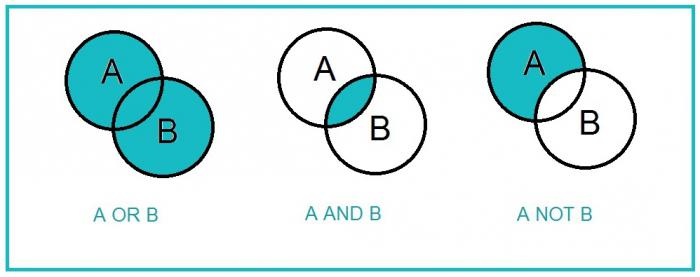
Операције Боолове алгебре

Већ се сећамо да су операције у алгебре пропозиција -логично. Као што алгебра бројева користи аритметичке операције за додавање, одузимање или упоређивање бројева, елементи математичке логике омогућавају састављање сложених изјава, одбијање или израчунавање коначног резултата.

Логичке операције за формализацију и једноставностсу записане формулама које су уобичајене за нас у аритметици. Својства Боолове алгебре омогућавају писање једначина и израчунавање непознатих. Логичке операције су обично написане помоћу табеле истине. Његови ступци дефинишу елементе израчунавања и операцију која се обавља на њима, а редови приказују резултат израчунавања.

Основне логичке акције

Најчешће у Боолеовој алгебриоперације су негација (НОТ) и логична АНД и ОР. Дакле, можете описати скоро све акције у алгебрима пресуда. Детаљно ћемо проучавати сваку од три операције.

Негација (не) се односи само на једнуелемент (операнд). Дакле, операција негације се назива уједначена. Да напишете концепт "не А", користите такве симболе: ¬А, А¯¯¯ или! У табеларном облику изгледа овако:

За функцију негације, типична је следећа наредба: ако је А тачно, онда је А лажно. На пример, Месец се врти око Земље - истина; Земља се врти око месеца - лаж.

Логичко множење и додавање

Логичан АНД се зове операција коњукције. Шта то значи? Прво, да се може применити на два операнда, то јест, ја сам бинарна операција. Друго, да само у случају истине оба операнда (и А и Б) сам израз је истинит. Преговарање "Стрпљење и рад ће перетрут" претпоставља да ће само два фактора помоћи особи да се суочи са тешкоћама.

Симболи се користе за снимање: А∧Б, А⋅Б или А && Б.

Коњункција је аналогна мултипликацији у аритметици. Понекад кажу тако - логично множење. Ако множимо елементе табеле по редовима, добијамо резултат сличан логичком мишљењу.

Дисјункција се назива логична ОР операција. Потребно је вриједност истине када је бар једна од изјава тачна (или А или Б). Пише се овако: А∨Б, А + Б или А || Б. Табеле истине за ове операције су:

Дисјункција је попут аритметичког додатка. Операција логичког додатка има само једно ограничење: 1 + 1 = 1. Али се сећамо да је у дигиталном формату математичка логика ограничена на 0 и 1 (где је 1 тачно, 0 је лажно). На пример, изјава "у музеју можете видети ремек-дело или упознати занимљивог саговорника" значи да можете видети уметничка дела, а можете се упознати са занимљивом особом. Истовремено, није искључена могућност истовременог остваривања оба догађаја.

Функције и закони

Дакле, ми већ знамо које су логичке операцијекористи Боолову алгебру. Функције описују сва својства елемената математичке логике и омогућавају вам да поједноставите сложене сложене услове задатака. Најопаснији и једноставнији је својство напуштања деривативних операција. Деривати су ексклузивни ОР, импликација и еквиваленција. Пошто смо се упознали само са основним операцијама, ми ћемо само узети у обзир њихове особине.

Асоцијативност значи да у изјавама попут "и А, Б, и Б", попис операнда није битан. Формула је ово:

(А∧Б) ∧ Б = А∧ (Б∧В) = А ∧ Б ∧ В,

(А∨Б) ∨ Б = А∨ (Б∨В) = А∨Б∨В.

Као што видимо, ово је карактеристично не само за везивање, већ и за дисјункције.

Комутативност тврди да резултат коњукције или дисјункције не зависи од тога који елемент је разматран на почетку:

А∧Б = Б∧А; А∨Б = БВА.

Дистрибутивност омогућава вам да отворите заграде у сложеним логичким изразима. Правила су слична откривању заграда када се множе и додају алгебри:

А∧ (Б∨В) = А∧Б∨А∧В; А∨Б∧Б = (А∨Б) ∧ (А∨Б).

Својства јединице и нула, који могу бити један од операнда, такође су аналогни алгебарском множењу са нулом или једним и додатком једне:

А∧0 = 0, А∧1 = А; А∨0 = А, А∨1 = 1.

Идемпотенција то нам говори ако двојеједнаки операнди, резултат операције се испоставља аналогним, онда је могуће "избацити" додатне операнде који компликују ток размишљања. И коњункција и дисјункција су идемпотентне операције.

БББ = Б; БББ = Б.

Апсорпција такође нам омогућава да поједноставимо једначине. Апсорпција каже да када се операција са истим операндом примјењује на израз са једним операндом, резултат је операнд из операције апсорпције.

А∧Б∨Б = Б; (А∨Б) ∧Б = Б.

Секвенца операција

Низ операција је важанзначење. Заправо, што се тиче алгебре, постоји приоритет функција које користе Боолеан алгебра. Формуле се могу поједноставити само ако се поштује значај операција. Рангирање од најзначајнијих до малих, добијамо следећи низ:

1. Одбијање.

2. Коњункција.

3. Дисјункција искључујући ОР.

4. Импликација, еквиваленција.

Као што можете видети, само негацију заједно и немају једнак приоритет. Приоритет дисјункције и КСОР једнаки, као и приоритете импликацији и еквиваленције.

Импликације и функције еквиваленције

Као што смо већ рекли, поред основних логичких операција, математичка логика и теорија алгоритама користе деривате. Најчешће коришћена импликација и еквивалентност.

Импликација или логично следиизјава у којој је једна акција услов, а друга је последица његовог испуњења. Другим речима, ова реченица са изговарањем "ако ... онда." "Волиш да возиш, волиш и сањаш да носиш". То јест, за клизање потребно је затегнути санкање на брдо. Ако нема жеље да напустите планину, онда не морате носити санкање. Пише се овако: А → Б или А⇒Б.

Еквиваленција претпоставља да је резултатАкција се дешава само када су оба операнда тачна. На пример, ноћ се замењује тадашњим даном (а тек тада), када сунце излази из хоризонта. На језику математичке логике, ова изјава је написана као: А≡Б, А⇔Б, А == Б.

Остали закони Боолове алгебре

Развија се пресудна алгебра, и многизаинтересовани научници формулисали нове законе. Најпознатији су постулати шкотског математичара О. де Морган. Приметио је и дефинисао таква својства као што је блиска негација, додатак и двострука негација.

Затвори Негатион сугерише да не постоји ниједна негација прије конзоле: не (А или Б) = не А или НЕ Б.

Када је операнд негиран, без обзира на њено значење, додатак:

Б ∧ Б = 0; Б¬¬Б = 1.

И, коначно, двострука негација компензује се. Ие. Пре операнда или негација нестаје, или само остаје.

Како решити тестове

Математичка логика подразумева поједностављењедатих једначина. Као и код алгебре, прво је неопходно учинити стање што лакше (ослободити се сложених увода и операција с њима), а затим наставити да пронађете прави одговор.

Шта можемо учинити да поједноставимо ствари? Претворите све изведене операције у једноставне. Затим отворите све заграде (или обрнуто, склоните заграде да бисте скратили овај елемент). Следећи корак је примена особина Боолове алгебре у пракси (апсорпција, особине нуле и јединице итд.).

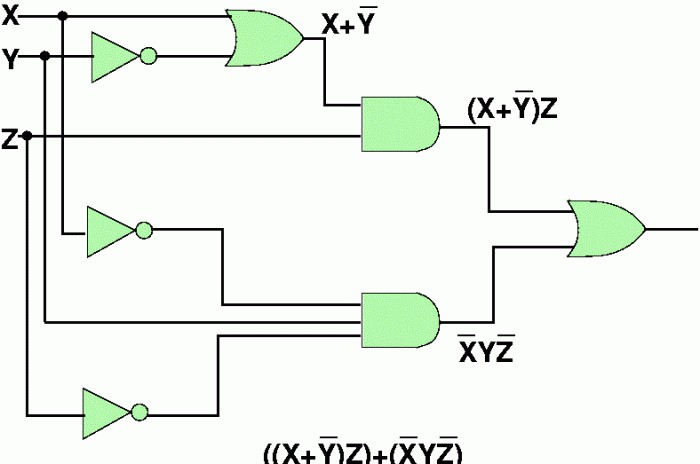
У коначној анализи, једначина мора бити састављенаМинимални број непознатих, уједињени једноставним операцијама. Најједноставније је тражити рјешење ако се постигне велики број блиских негација. Тада ће се одговор појавити као по себи.