Конвексни полигони. Дефиниција конвексног полигона. Дијагонали конвексног полигона

Ове геометријских облика су свуда око нас. Конвексна полигони су природни, као што је саће или вештачке (човек направио). Ове фигуре се користе у производњи различитих врста премаза, у сликарству, архитектури, декорацијама итд. Конвексни полигони имају својство да се све њихове тачке налазе на једној страни линије која пролази кроз пар суседних вертикала ове геометријске фигуре. Постоје и друге дефиниције. Конвексни је тај полигон који се налази у једној полу-равни према било којој линији која садржи једну од његових страна.

Конвексни полигони

У току елементарне геометрије, увексматрамо само једноставним полигонима. Да би се схватиле све особине таквих геометријских фигура неопходно је разумјети њихову природу. За почетак, требало би схватити да свака линија чији се крајеви поклапају назива се затворена. И фигура коју она формира може имати различите конфигурације. Полигон је једноставна затворена полигонална линија чије суседне везе не леже на истој линији. Његове везе и врхови су, у суштини, стране и вертикала ове геометријске фигуре. Једноставна полилина не сме да има самоповршења.

Точке полигона се називају суседне, у том случајуако представљају крајеве једне од својих страна. Геометријска фигура која има н-ти број вертиса, а самим тим и н-ти број страна, назива се н-гон. Ломљена линија се зове граница или контура ове геометријске фигуре. Полигонска равнина или полигон равни се назива коначни део било које равниће која је ограничена њиме. Суседне стране ове геометријске фигуре су сегменти преломљене линије, почевши од једне тачке. Они неће бити суседни ако долазе из различитих вертиката полигона.

Друге дефиниције конвексних полигона

У елементарној геометрији постоје још неколикоеквивалентан по значењу дефиниција, указујући на који полигон се назива конвексан. А све ове формулације су једнако тачне. Конвексни полигон се сматра:

• сваки сегмент који повезује било које две тачке унутар ње у потпуности лежи у њему;

• унутар ње леже све дијагонале;

• сваки унутрашњи угао не прелази 180 °.

Полигон увек дели авион за 2делови. Један од њих је ограничен (може бити затворен у круг), а други неограничен. Прва се зове унутрашња област, а друга се зове спољашња област ове геометријске фигуре. Овај полигон је раскрсница (другим речима - заједничка компонента) неколико полупроизвода. У овом случају, сваки сегмент који се завршава на тачкама који припадају полигону у потпуности припада њему.

Варијанте конвексних полигона

Дефиниција конвексног полигона не указује на точињеница да постоје многе врсте њих. И свака од њих има одређене критеријуме. Тако, конвексна полигони који имају унутрашњи угао од 180 °, из благо конвексна. Конвексна геометријска фигура која има три врхове, се зове троугао, четири - четвороугао, пет - Пентагон, итд Сваки конвексне н-гон испуњава следеће важне услове: .. Н мора бити једнака или већа од 3. Сваки од троуглова конвексна. Геометријски фигура овог типа у којем су сви темена налази на кругу, под називом уписан круг. Описано конвексна полигон се зове ако сви њени стране око круга да је додирнете. Два полигона се називају једнаки само у случају када се користи преклапање се може комбиновати. Стан полигон под називом многоугаоника раван (авион део) који овом ограниченом геометријске фигуре.

Редовни конвексни полигони

Зову се исправни полигонигеометријске фигуре са једнаким угловима и странама. Унутар њих постоји тачка 0, која је на истој удаљености од сваке његове вертикале. Зове се центар ове геометријске фигуре. Сегменти који повезују центар са вертикама ове геометријске фигуре се зову апопхемес, а они који повезују тачку 0 са странама су радије.

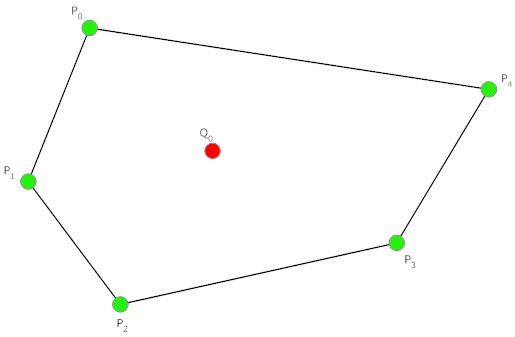
Прави четвороугао је квадрат. Прави троугао се назива једнакостраним. За такве цифре постоји следеће правило: сваки угао конвексног полигона је 180 ° * (н-2) / н,

где је н број вертиса ове конвексне геометријске фигуре.

Површина било ког регуларног полигона је дефинисана формулом:

С = п * х,

где је п једнак половини суме свих страна датог полигона, а х је једнак дужини апопхеме.

Својства конвексних полигона

Конвексни полигони имају одређена својства. Дакле, сегмент који повезује било које две тачке такве геометријске фигуре, нужно се налази у њему. Доказ:

Претпоставимо да је П дат конвексанполигон. Узмите две произвољне тачке, нпр и Б, које припадају П. По тренутном дефиниције конвексне полигона, ове тачке се налазе на једној страни праве линије која садржи одређену правац Р. Према томе, АБ такође има ову особину и садржан у Р. конвексног полигона увек могу се поделити у неколико троуглове апсолутно све дијагонала, који су држали један од његових темена.

Углови конвексних геометријских фигура

Углови конвексног полигона су углови тогаформирају своје партије. Унутрашњи углови су у унутрашњој површини ове геометријске фигуре. Угао који се формира са стране, који се конвергира на једној тачки, назива се угао конвексног полигона. Углови поред унутрашњих углова одређене геометријске фигуре се називају спољашњим. Сваки угао конвексног полигона који се налази унутар ње је једнак:

180 ° - к,

где је к вредност вањског угла. Ова једноставна формула се примјењује на све геометријске фигуре ове врсте.

У општем случају, постоји за вањске угловеследеће правило: сваки угао конвексног полигона је једнак разлици између 180 ° и вриједности унутрашњег угла. Може имати вриједности у распону од -180 ° до 180 °. Стога, када је унутрашњи угао 120 °, спољашњи угао ће бити 60 °.

Сума углова конвексних полигона

Сума унутрашњих углова конвексног полигона утврђује се према формули:

180 ° * (н-2),

где је н број вертиса н-гона.

Израчунава се збир углова конвексног полигонаприлично једноставно. Размотрите било какву геометријску слику. Да би се одредила сума углова унутар конвексног полигона, једна од његових вертикала мора бити повезана са другим врховима. Као резултат ове акције добијамо (н-2) троуглове. Познато је да је збир углова било ког троугла увек 180 °. Пошто је њихов број у било којем полигону једнак (н-2), збир унутрашњих углова такве фигуре је 180 ° к (н-2).

Сума углова конвексног полигона, виз.било која два унутрашња и суседна екстерна угла, ова конвексна геометријска слика увек ће бити 180 °. Из овога се може утврдити збир свих углова:

180 х н.

Сума унутрашњих углова је 180 ° * (н-2). Из овога, сума свих спољашњих углова датог броја утврђује се формула:

180 ° * н-180 ° - (н-2) = 360 °.

Сума спољашњих углова било ког конвексног полигона увек ће бити 360 ° (без обзира на број његових страна).

Спољни угао конвексног полигона генерално представља разлику између 180 ° и вриједности унутрашњег угла.

Друга својства конвексног полигона

Осим основних особина ових геометријскихфигуре, они имају друге који настају када их манипулишу. Према томе, било који полигон може се подијелити на неколико конвексних н-гона. Због тога је неопходно наставити са сваке стране и смањити ову геометријску фигуру дуж ових правих линија. Раздвојите било који полигон на неколико конвексних делова и на такав начин да се вертикали сваког од делова подударају са свим његовим вертикама. Из ове геометријске слике веома је једноставно направити троуглове држећи све дијагонале из једне тачке. Стога, било који полигон, у коначној анализи, може се подијелити на одређени број троуглова, што је врло корисно у рјешавању различитих проблема везаних за такве геометријске фигуре.

Периметар конвексног полигона

Комади полилина, названи су странеполигон, најчешће означен словима: аб, бц, цд, де, еа. Ово су стране геометријске фигуре са вертикама а, б, ц, д, е. Сума дужине свих страна овог конвексног полигона назива се њеним периметром.

Круг полигона

Конвексни полигони се могу уписати иописани. Круг који додирује све стране ове геометријске фигуре се назива уписаним у њега. Такав полигон се назива описан. Средиште круга које је уписано у полигон је тачка пресека бисектора свих углова унутар одређене геометријске фигуре. Подручје таквог полигона једнако је:

С = п * р,

где је р радијус уписаног круга, а п је семипериметар датог полигона.

Круг који садржи вертикале полигона,названу близу њега. У овом случају ова конвексна геометријска фигура се назива уписаним. Центар круга, који је описан у близини таквог полигона, представља тачку пресека тзв. Средњих праваца на свим странама.

Дијагонале конвексних геометријских фигура

Дијагонали конвексног полигона су сегменти,која повезује не суседне вертикале. Свака од њих лежи унутар ове геометријске фигуре. Број дијагонала таквог н-гона утврђује се према формули:

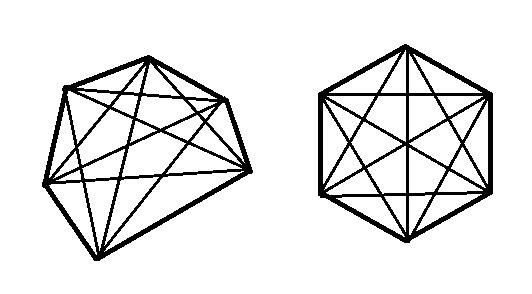
Н = н (н-3) / 2.

Број дијагонала конвексног полигонаважна улога у елементарној геометрији. Број троуглова (К), у који се може поделити сваки конвексни полигон, израчунава се према следећој формули:

К = н - 2.

Број дијагонала конвексног полигона увек зависи од броја његових вертикала.

Раздвајање конвексног полигона

У неким случајевима, ријешити геометријскинеопходно је поделити конвексни полигон у неколико троуглова са дисјоинтованим дијагоналама. Овај проблем се може решити добивањем одређене формуле.

Дефиниција проблема: ми именујемо одређену партицију конвексног н-гона у неколико троуглова дијагоналима који се пресецају једино у вертикалама ове геометријске фигуре.

Решење: Претпоставимо да су П1, П2, П3 ..., Пн вертицес овог н-гона. Број Ксн је број његових партиција. Пажљиво размотрите резултирајућу дијагоналу геометријске фигуре Пи Пн. У било којој од редовних партиција П1 Пн припада одређеном троуглу П1 Пи Пн, за који 1 <и <н. Полазећи од овога и претпостављајући да и = 2,3,4 ..., н-1, добијамо (н-2) групе ових партиција, у које су укључени сви могући посебни случајеви.

Нека је и = 2 једна редовна групакоји увек садржи дијагонално П2 Пн. Број партиција који улазе у њега поклапа се са бројем партиција (н-1) -гон П2 П3 П4 ... Пн. Другим речима, то је једнако Ксн-1.

Ако је и = 3, онда ће ова друга група партиција битиувек садрже дијагонале П3 П1 и П3 Пн. Штавише, број редовних партиција који се налазе у овој групи ће се подударати с бројем партиција (н-2) -гон П3 П4 ... Пн. Другим речима, то ће бити једнако Ксн-2.

Нека је и = 4, онда је међу троугловима редованразлагање ће нужно садржати троугао П1 П4 Пн у који се придружи четвороугаока П1 П2 П3 П4, (н-3) -гон П4 П5 ... Пн. Број редовних партиција таквог квадрилата једнак је Кс4, а број партиција (н-3) -гона једнак је Ксн-3. На основу свега наведеног, можемо рећи да је укупан број редовних партиција који се налазе у овој групи Ксн-3 Кс4. Друге групе за које и = 4, 5, 6, 7 ... садрже Ксн-4 Кс5, Ксн-5 Кс6, Ксн-6 Кс7 ... регуларних партиција.

Нека и = н-2, тада број редовних партиција у датој групи поклапаће се с бројем партиција у групи за коју и = 2 (другим речима, то је једнако Ксн-1).

Пошто је Кс1 = Кс2 = 0, Кс3 = 1, Кс4 = 2 ..., онда је број свих партиција конвексног полигона једнак:

Ксн = Ксн-1 + Ксн-2 + Ксн-3 Кс4 + Ксн-4 Кс5 + ... + Кс 5 Ксн-4 + Кс4 Ксн-3 + Ксн-2 + Ксн-1.

Пример:

Кс5 = Кс4 + Кс3 + Кс4 = 5

Кс6 = Кс5 + Кс4 + Кс4 + Кс5 = 14

Кс7 = Кс6 + Кс5 + Кс4 * Кс4 + Кс5 + Кс6 = 42

Кс8 = Кс7 + Кс6 + Кс5 * Кс4 + Кс4 * Кс5 + Кс6 + Кс7 = 132

Број редовних партиција пресецају једну дијагоналу

У верификацији појединих случајева може се претпоставити да је број дијагонала конвексних н-гона једнак производу свих партиција ове фигуре помоћу (н-3).

Доказ ове претпоставке: представљамо да је П1н = Ксн * (н-3), онда се сваки н-гон може разградити у (н-2) -триангле. Истовремено, један од њих се може комбиновати (н-3) - четверокут. Поред тога, сваки квадрилатер ће имати дијагоналу. Пошто се на овој конвексној геометријској слици могу извући двије дијагонале, то значи да је могуће извући додатне дијагонале (н-3) у било који (н-3) -тво-лапарон. Из овога се може закључити да је у свакој редовној партицији могуће извести (н-3) -диагоне који одговарају условима овог проблема.

Површина конвексних полигона

Често решавајући разне проблеме, елементарногеометрија, постаје неопходно одредити област конвексног полигона. Претпоставимо да је (Кси. Ии), и = 1,2,3 ... н секвенца координата свих суседних вертикала полигона који нема самоповршења. У овом случају његова површина се израчунава према следећој формули:

С = 1 (Σ (Кс_и + Кс_{и + 1}) (И_и + И_{и + 1})),

где (Кс₁, И₁) = (Кс_{н +1}, И_{н + 1}).

</ п>